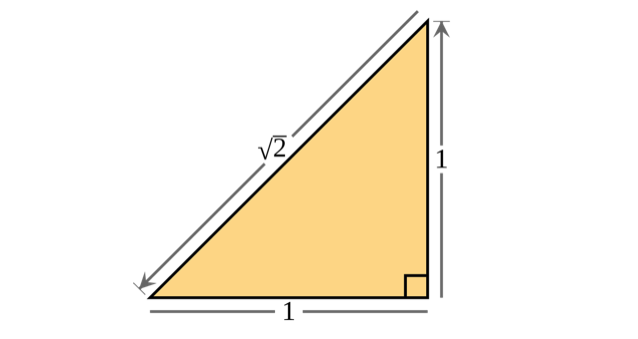
İşte matematik tarihinin en zarif kanıtlarından biri. \( \sqrt{2} \)'nin irrasyonel bir sayı olduğunu, başka bir deyişle \( a\) ve \( b\)'nin tam sayı olmak üzere bir \(a/b \) kesri olarak yazılamayacağını gösteriyor.
√2'nin a/b kesri olarak yazılabileceğini ve a ve b' nin ortak bir böleninin olmadığını varsayarak başlarız - eğer varsa sadeleştiririz.
Sembolle gösterilirse:
\( \frac{a}{b} = \sqrt{2}. \)
Her iki tarafın karesini alırsak
\( \frac{a^2}{b^2} = 2 \)
elde ederiz. Ve her iki tarafı \( b^2 \) ile çarparsak
\( a^2 = 2b^2.\)
Bu, \( a^2 \) 'nin çift sayı olduğu anlamına gelir: \(2 \)'nin bir katıdır. Şimdi eğer \( a^2 \) çift sayı ise, \( a \) da çift olur (tek bir sayının karesinin tek olduğunu kendiniz kontrol edebilirsiniz). Bu, \( a \)'nın, \( c \) başka bir tam sayı olmak üzere \( 2c \) olarak yazılabileceği anlamına gelir. Bu nedenle,
\( 2b^2 = a^2 = (2c)^2 = 4c^2. \)
\(2 \)'ye bölersek
\( b^2 = 2c^2. \)
Bu, \( b^2 \) 'nin çift olduğu anlamına gelir, bu da yine \( b\)'nin de çift olduğu. Bununla birlikte hem \( a \) hem de \( b \) çifttir, bu da ortak bir bölen içermediği varsayımıyla çelişir: eğer her ikisi de çiftse, \(2 \) ortak bölenine sahiptirler. Bu çelişki, \( \sqrt{2} \)'nin bir \( a/b \) kesri olarak yazılabileceği varsayımımızın yanlış olmasını gerektirir. Bu nedenle, \( \sqrt{2} \) irrasyoneldir.
Kaynak:
Maths in a minute: The square root of \(2 \) is irrational, https://plus.