Olağanüstü üretken bir matematikçi olan Euler’in yaşamı boyunca yaklaşık 550 kitap ve makalesi yayınlanır. Tüm bilimsel eserleri 850 civarındadır. 1909'da İsviçre Doğa Bilimleri Akademisi, Euler’in çeşitli ülkelerde ortaya koyduğu bütün çalışmalarını topladığı eserlerin yayınlanmasını üstlenir. Ancak 1975 yılında tamamlanabilen baskı 72 ciltten oluşuyor. Sovyetler Birliği Bilimler Akademisi de 1963 yılında bilimsel açıdan oldukça kıymetli, yaklaşık 3.000 mektuptan oluşan Euler'in yazışmalarını yayınlar.
Euler bu eşsiz üretkenliğini birçok bilim dalında gerçekleştirir. Zamanının matematiğinin tüm dallarına ek olarak çalışmaları, mekanik, matematiksel fizik, optik, esneklik kuramı, müzik kuramı, balistik ve deniz bilimi konularını içerir. Bu bağlamda Euler'in eserlerinin yaklaşık beşte üçü matematiğe, kalan beşte ikisi ise matematiğin uygulamalarına aittir.
ÇOKYÜZLÜ NEDİR?
Euler’in çokyüzlü formülünü ortaya koymadan önce çokyüzlü kavramını tanımakla başlayalım. Geometrik bir nesne olan çokyüzlü bütün yüzleri düzlemsel çokgenlerle sınırlanmış kapalı ve deliksiz bir katı cisimdir. Mesela küp (altıyüzlü) Şekil 1’de görüldüğü üzere altı tane kare ile sınırlanmış bir katı cisimdir. Küp 8 köşe, 12 kenar ve 6 yüzden oluşur.
EULER'İN MAKALESİNİN KAVRAMLARI
Aşağıda ne anlama geldiğini berraklaştıracağımız formül, Euler tarafından 1752’de, Commentarii Academiae Scientiarum Imperialis Petropolitanae isimli dergide yayımlanan Katı cisimlerin doktrininin ögeleri (Elementa doctrinae solidorum) başlıklı Latince makalede ortaya konulur.
Altmış beş maddeden oluşan makalenin ilk altısında Euler, konuya bir giriş yapar ve katı cisimler geometrisinin düzlem geometrisiyle ilişkisini açıklar. Euler yedinci maddede formülün yapı taşlarını oluşturacak kavramları sunuyor. Bunlar:
- Anguli solidi (katı cisim açısı): Makaledeki niceliksel gösterimi S. Günümüzde V (İngilizce vertex sözcüğünün ilk harfi) ile gösteriyoruz.
- Acies (kenar): Makaledeki niceliksel gösterimi A. Günümüzde E (İngilizce edge sözcüğünün ilk harfi) ile gösteriyoruz.
- Hedrae (yüz): Makaledeki niceliksel gösterimi H. Günümüzde F (İngilizce face sözcüğünün ilk harfi) ile gösteriyoruz.
Euler bunlara ek olarak iki nicelik daha tanımlıyor. Bu niceliklerden ilki olan düzlem açısı (anguli planius), verilen bir çokyüzlünün yüzlerini oluşturan çokgenlerin düzlem açılarının sayısını ölçer. Örneğin, bir kare dört düzlem açısından oluşur. Sekiz köşeden meydana gelen bir küpün her köşesinde üç kare bir araya geldiği için toplam yirmi dört düzlem açısı vardır. İkinci tanımlanan nicelik ise çokgen kenarı (laternum) olarak tanımlanır. Yine küp örneğine dönecek olursak, bir küp altı tane kare yüze sahiptir. Her bir kare dört kenardan oluştuğu için küpün çokgen kenarı sayısı yirmi dört olur. Euler, bu nicelikler için değişken kullanmasa da biz sırasıyla, Latince baş harflerini referans alarak, P ve L ile gösterebiliriz. Küp için bu iki niceliğin birbirine eşit olduğunu gördük. Euler, Madde 8’de başka bir örnek ile sunduğu bu gözlemi, Önerme 1’de her çokyüzlü için kanıtlıyor, yani Öneme 1: P = L.
Tüm kenar uzunlukları ve açıları birbiriyle eş olan çokgenleri düzgün çokgen olarak adlandırıyoruz. Benzer şekilde düzgün çokyüzlü bütün yüzleri bir tür düzlemsel düzgün çokgenlerle sınırlanmış bir katı cisimdir. Euler dokuzuncu maddede günümüzde Platonik cisimler olarak bilinen beş düzgün çokyüzlüden bahsediyor. Bunlar sırasıyla dörtyüzlü, altıyüzlü (küp), sekizyüzlü, onikiyüzlü ve yirmiyüzlüdür.
Madde 11 ve 12’de çokyüzlüleri nasıl sınıflandıracağımıza öneriler sunan Euler, bu çok yüzlülerin yanı sıra üçgen piramit, üçgen prizma ve paralelyüzlü katı cisimlerinden bahsediyor. Sonraki maddelerde konuya dair genel tartışmalarını sürdüren Euler, Madde 21’de makalesinin Önerme 1’ini (Şekil 1) ortaya koyuyor:

Önerme 1. Herhangi bir katı cisimde, kenarların sayısı, yüzlerin köşelerinde bulunan düzlem açılarının sayısının yarısıdır.
Matematiksel dilde Önerme 1 şu hali alıyor: E = P/2. Küp örneğine dönecek olursak, 12 = 24/2. Madde 22, Madde 23, 24 ve 25’te Önerme 1’in sonuçları ifade ediliyor. Bunu takiben Madde 26’da Önerme 2’yi (Şekil 2) görüyoruz:

Önerme 2. Tüm düzlem açılarının sayısı ya tüm yüzlerin toplamının sayısının üç katına eşittir ya da ondan daha büyüktür. Düzlem açılarının sayısı hiçbir zaman bir katı cisim etrafındaki yüz sayısının üç katından daha az olamaz.
Matematiksel dilde Önerme 2’yi şöyle ifade edebiliriz: Ya P = 3F yada P > 3F. Asla P 3V ’dir. Asla P 3V’dir. Asla 2E
EULER'İN ÇOKYÜZLÜ FORMÜLÜ: S – A + H = 2 ya da V – E + F = 2
Bu da bizi Madde 33’te Önerme 4 (Şekil 3) olarak ifade edilen Euler’in çokyüzlü formülüne getiriyor:

Önerme 4. Düzlemlerle çevrelenmiş herhangi bir katı cisim içinde, katı cismin açıların sayısı ile yüzlerin sayısının toplamı yüzlerin sayısından 2 fazladır. Yani, S + H = A + 2
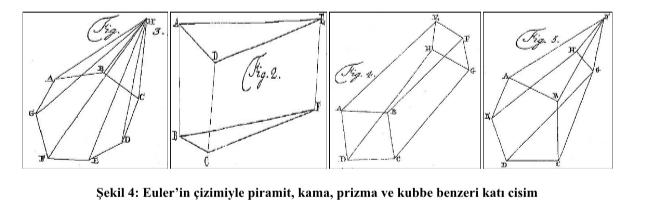
Güncel matematiksel gösterim ile ifademiz V + F = E + 2 halini alıyor. Euler, bu teoremin kesin bir kanıtı olmadığını hemen itiraf ediyor. Ancak Euler, bu formülü piramitler, kamalar (wedges), prizmalar ve kubbe benzeri katı cisimler için geçerli olduğunu kanıtlar. Bu katı cisimler şöyle tarif edilebilir (Şekil 4):
- Piramitler, köşeleri tek bir noktaya bağlanmış bir n-gen tabana sahiptir.
- Kamalar, bir çizgi parçasının iki uç noktasından birine bağlı köşelere sahip bir n-gen tabana sahiptir.
- Prizmalar, başka bir n-genin köşelerine bağlı köşeleri olan bir n-gen tabana sahiptir.
- Kubbe benzeri katı cisimler, bir m-genin köşelerine bağlanmış köşelere sahip bir n-gen tabana sahiptir.
Euler Önerme 4’ü Platonik cisimler için kanıtlayarak tamamlar. Madde 59’a kadar çeşitli önermeleri ve sonuçları ortaya koyan Euler, Madde 59’da (Şekil 5) büyük problemi ortaya koyuyor: Tüm katı cisimleri sınıflandırmak. Diğer maddelerde bunun nasıl yapılabileceğini örneklerden üzerinden tartışıyor ve problemin kimi sonuçlarını listeliyor.
Euler bir yıl sonra yayınladığı makalede problemin ikna edici bir çözümünü dışbükey çokyüzlüler için sunar. Ancak bu çözümü, Euler’in çokyüzlü formülünün kanıtını ve Descartes’in bu formüle dair ön çalışmalarını bir sonraki yazıya bırakalım. Yazıyı noktalandırmadan önce Euler’in çokyüzlü formülünün Şekil 6’teki platonik cisimlerde nasıl çalıştığını görelim.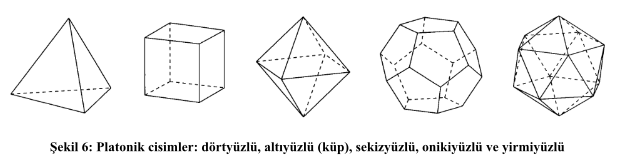
Dörtyüzlü için V = 4, E = 6 ve F = 4, dolayısıyla V – E + F = 2. Küp için bu nicelikleri tespit etmiştik, sağlandığını hızlıca görebilirsiniz. Sekizyüzlüde 6 köşe, 12 kenar ve 8 yüz var, demek ki V – E + F = 2. Diğer iki çokyüzlü için de Euler’in çokyüzlü formülünün sağlandığını görmek okuyucuya ödev olsun. Ben bununla yetinmem diyen okuyucuya biraz daha zor bir ödev verelim: Euler’in çokyüzlü formülünü kullanarak, platonik cisimlerden başka bir düzgün dışbükey çokyüzlü bulunamayacağını kanıtlayın.
Kaynaklar:
L. Euler - Elementa doctrinae solidorum, Novi Commentarii Academiae Acientiarum Petropolitanae 4 (1752/3) 1758, p. 109-140, reprinted in Opera Omnia, Series I, Vol. 26, p. 71-93.
P. S. Aleksandov – Leonhard Euler, Great Soviet Encyclopedia, Macmillan Publishers, Third Edition, 1979.
L. Stemkoski - Investigating Euler's Polyhedral Formula Using Original Sources, Convergence, 2010.
E. Sandfier – How Euler Did It, V, E and F, Part 1, Mathematics Association of America, 2006.
E. Sandfier – How Euler Did It, V, E and F, Part 2, Mathematics Association of America, 2006.
P. R. Cromwell - Polyhedra, Cambridge University Press, 1997.