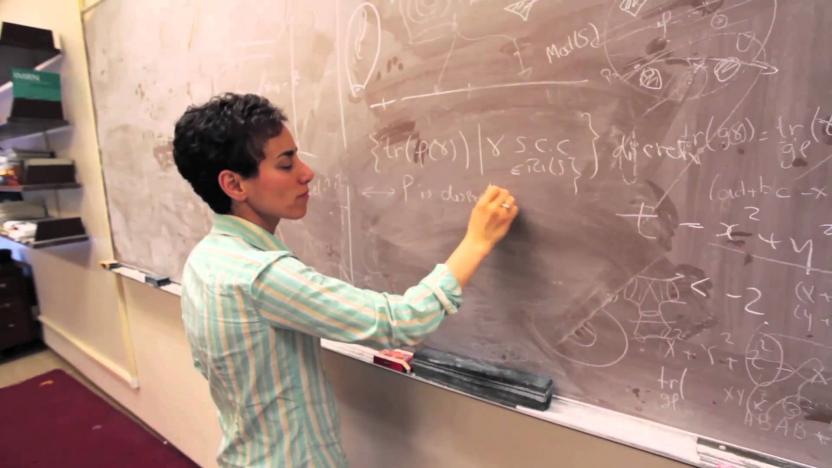1977 yılında Tahran'da doğan matematikçi Meryem Mirzakhani, 15 Temmuz 2017 günü yaşama veda etti. 2014 yılında Seul'de düzenlenmiş olan Uluslararası Matematik Kongresi’nde “Riemann yüzeylerinin ve bu yüzeylerin moduli uzaylarının dinamiği ve geometrisine yaptığı önemli katkılar” nedeniyle Mirzakhani'ye Fields madalyası verilmişti. Dahası, Mirzakhani,bu ödülü alan ilk kadın matematikçidir. Şimdi Mirzakhani'nin doktora sonrası sadece 13 yıl sürmüş olan kısa fakat son derece yaratıcı araştırma yaşamı süresince matematiğe, araştırma sahası olan geometriye, yapmış olduğu muazzam katkıları kısaca anlatmaya çalışalım.
Yüzeyler (her zaman R3 içinde kabul edeceğiz) topolojik olarak bulundurdukları “kulp” sayılarına (=delik sayılarına) göre sınıflandırılır. Bir S yüzeyinin kulp sayısına da bu yüzeyin “cinsi” denir. Yani herhangi bir S yüzeyini “deforme ettirerek” (=kesmeden, yırtmadan) küre (cinsi 0), simit (cinsi 1) gibi standart yüzeylerden sadece birisine, oyun hamuru ile oynayan çocuk örneğinde olduğu gibi, dönüştürmek mümkündür.
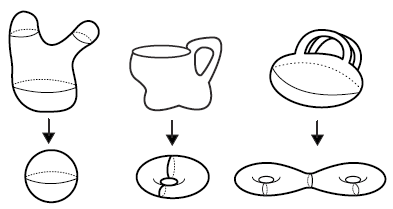
Görsel kaynağı: https://www.learner.org/courses/mathilluminated/units/4/textbook/03.php
Eğer bir S yüzeyi, üzerinde kompleks analiz (=kompleks sayılar ile hesaplamalar) yapılabilecek bir “kompleks yapı” ile donatılmış ise, yani kabaca her S’nin elemanı olan her p noktasının bir U açık komşuluğu C kompleks sayılar düzleminin bir Uc açık kümesi ise, S'ye bir Riemann yüzeyi denir.
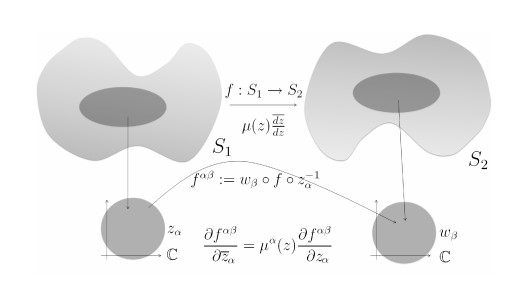
Görsel kaynağı:W. Zeng, L.M. Lui, F. Luo, J.S. Liu T.F. Chan, S.T. Yau, X.F. Gu, "Computing Quasiconformal Maps on Riemann surfaces using Discrete Curvature Flow", arXiv:1005.4648 [math.NA]
Öte yandan Riemann yüzeyini, S yüzeyi üzerine “konform yapı” ile, yani üzerinde açı ölçümü, uzunluk ve alan hesaplaması yapılabilecek bir “metrik” (=uzunluk fonksiyonu) ile donatarak da tanımlamak mümkündür. Bu durumda S'ye bir hiperbolik yüzey denmektedir.

Görsel kaynağı:http://www.belloma.it/geometrie-non-euclidee-lobachevski-bolyai-e-gauss-...
Dolayısıyla bir S hiperbolik yüzeyinin üzerinde, üzerindeki herhangi iki noktanın en kısa uzunlukta olacağı, “jeodezik eğriler” inşa etmek mümkündür. Özellikle, asal sayılarla benzerliklerinden dolayı S üzerinde asal, yani kapalı ve primitif (=tek döngülü) jeodezik eğriler son derece önemlidir. Bu yönde 1969 yılında ilk olarak Margulis (daha sonra Sarnak'ın tezinde geliştirdiği) kapalı ve primitif jeodezik eğriler için bir “asal sayılar teoremi” ispatlamıştır. Şöyle ki, bu teorem, S hiperbolik yüzeyi üzerinde c uzunluğundan kısa olan kapalı primitif jeodezik eğrilerin sayısının asimtotik olarak ec/c olduğunu söylemektedir.
Mirzakhani, ilk olarak S hiperbolik yüzeyi üzerindeki asal jeodezik eğriler kümesinin bir alt kümesi olan basit (yani kesişimsiz kapalı ve primitif) jeodezik eğriler için bir “asal sayılar teoremi” geliştirmiştir. Burada, S hiperbolik yüzeyinin üzerindeki asal jeodeziler ile Q sayı cismindeki asal sayılar arasındaki benzerlik, S üzerindeki basit jeodeziler ile Q cisminin sonlu genişlemelerinde asallığı bozulan asal sayılar arasındaki anolojiye dönüşmektedir. Mirzakhani, S hiperbolik yüzeyi üzerinde c uzunluğundan kısa olan basit jeodezik eğrilerin sayısının asimtotik olarak k.c6g-6 olduğunu ispat etmiştir. Burada k sayısı S yüzeyinin hiperbolik yapısından gelen belli bir sabiti, g sayısı da S yüzeyinin cinsini göstermektedir.
Cinsi g olan tüm Riemann yüzeyleri üzerinde “analitik olarak denk olmak” bir denklik bağıntısı tanımlar. Bu bağıntının denklik sınıflarından oluşan Mg kümesine cinsi g olan Riemann yüzeylerinin “moduli uzayı” denir. Elbette noktaları Riemann yüzeylerini sınıflandıran bu uzayın çok karmaşık bir yapısı vardır. Öte yandan, Mg uzayının kesiksiz olduğu, üzerinde simplektik yapı ile doğal bir metriğin, ve bu metrikle tanımlı jeodezik eğrilerin, varlığı bilinmektedir. Bu Mg uzayının simplektik yapısı ile Mg uzayında hacim (Weil-Petersson hacmi) hesaplamak mümkündür. Mirzakhani, Mg uzayında hacim hesabı ile bu uzayın bir noktasına karşılık gelen hiperbolik yüzeyin üzerinde bulunan c uzunluğundan kısa olan basit jeodezik eğrilerin sayısı arasında bir ilişki olduğunu gözlemlemiş ve sonuç olarak basit jeodezik eğriler için asal sayılar teoremini ispat etmiştir.
Daha sonra Mirzakhani, cinsi g olan bir Riemann yüzeyi üzerindeki basit jeodeziler için elde ettiği asal sayılar teoremini kullanarak ve bu yönde geliştirmiş olduğu Mg uzayı üzerinde hacim hesaplama tekniğini kullanarak, Kontsevich'in 1992 yılında ispatlamış olduğu, cinsi g olan Riemann yüzeylerinin Mg moduli uzayı için karakteristik sınıfları (=belli kohomoloji sınıfları) ile ilgili “Witten Sanıtını” Riemann yüzeyleri üzerindeki basit jeodezikleri sayma problemine indirgeyip ispat eder. Ayrıca, moduli uzayı Mg üzerindeki basit jeodezik eğriler için de bir asal sayılar teoremi geliştirir.
Mirzakhani'nin son çalışmaları, Mg uzayı üzerinde zamanla değişen sistemler, yani Mg üzerine dinamik sistemler ile ilgilidir. Bu yönde Mirzakhani, Alex Eskin ve Amir Mohammadi ile beraber, gene çok kısa bir süre önce 7 Temmuz 2017'de hayata veda eden, Marina Ratner'in homojen uzaylar üzerine dinamik sistemler için geliştirmiş olduğu teorinin anologunu Mg uzayı için geliştirmiştir. Dahası, Mirzakhani ile çalışma arkadaşları Eskin ve Mohammadi homojen uzaylar ile moduli uzayları tamamen zıt geometrik özelliklere sahip olsalar bile üzerlerindeki dinamik sistemlerin benzeri özelliklere sahip olduklarını gösterdiklerinden dolayı bahsi geçen çalışma bu alanda araştırma yapan matematikçileri çok heyecanlandırmıştır.
Cebirsel geometri, analiz, topoloji hatta olasılık gibi çeşitli konuların son derece güçlü tekniklerini rahatlıkla kullanabilen Mirzakhani, Riemann yüzeyleri ve bunların moduli uzayları ile ilgili temel sonuçlar elde etmiştir ve bu sahada çalışan matematikçilere yeni araştırma alanları açmıştır. Genç sayılacak bir yaşta aramızdan ayrılması matematik camiası için boşluğu doldurulmayacak büyük bir kayıptır.
Kaynaklar:
“The work of Maryam Mirzakhani”, IMU News release 2014.
A. Zorich, “Le théorème de la baguette magique de A. Eskin et M. Mirzakhani”, Gazette des mathématiciens, vol.142, 2014, 39–54.